你必然知道“摩尔定理”，对很多IT人而言那是这个行业最基本法例，然而，在我看来，另一个和摩尔定理齐名的“梅特卡夫定律”被严重地低估了。

和摩尔定理指出硬件机能进化逻辑差异，“梅特卡夫定律”在业务业务层面临互联网时代的成长纪律举办了高度归纳综合的总结，这个一抽象总结在已往、此刻和将来城市继承指引互联网的成长偏向。

一、什么是“梅特卡夫定律”
“梅特卡夫定律”的表述很是简朴——一个网络的代价和这个网络节点数的平方成正比，用公式表述就是：V=K×N²，个中V代表一个网络的代价，N代表这个网络的节点数，K代表代价系数。那么，这个看似极其简朴的公式为什么会受到互联网人如此高度的推崇呢？在答复这个问题之前，我们照旧简朴来相识一下“奇人”梅特卡夫：罗伯特·梅特卡夫1946年出生于纽约布鲁克林，年青时的梅特卡夫是一个尺度的学霸，在麻省理工得到了工程学和打点学的双学位，之后又在哈佛得到了博士学位，结业后他迅速插手了其时的科技巨头施乐。在施乐事情期间，他发现了当今局域网利用最遍及的协议之一——以太网，赣州九鼎广告，这让他年龄轻轻就一跃成为“计较机先驱”。
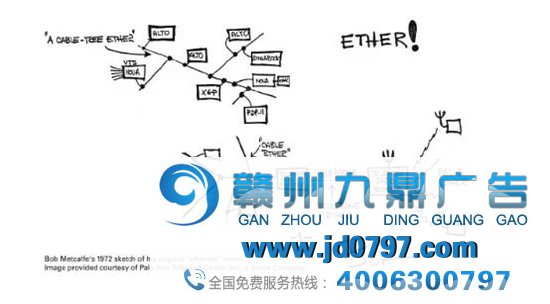梅特卡夫于1973年绘制的以太网草图
然而年青的梅特卡夫并没有躺在这一成就上坐吃山空，而是在人生33岁的时候抉择把本身把握的技能转酿成贸易产物，1979年，他开办了著名的3Com公司。3Com公司是做什么呢？通讯基本设施，你可以领略为美国的华为（事实上3Com厥后还和华为创立过合伙公司）。在打点3Com公司销售团队的时候，梅特卡夫发明其时客户对他们的主力网卡乐趣不大，这时候他展示了本身作为技能人超强的逻辑说服本领，他亲廉价作了一张幻灯片，画了一张图，列出了网络代价和本钱之间的干系。他想通过这张简朴图清楚地说服客户——买网卡的本钱跟着时间是线性增长的（N），但网卡组成的网络代价则是呈指数级增长的（N²）。言外之意就是你们此刻买网卡会以为不划算，但跟着买的人越来越多，它的回报将是指数级的。作为3Com公司的头号推销员，梅特卡夫在美国科技界的各个场所都在宣传他的这一理念，这引起了一位叫乔治·吉尔德的科技专栏作者的留意，吉尔德恒久在科技界浸润，直觉汇报他这页其貌不扬的PPT里大概藏着一个极具代价的判定。1993年，乔治·吉尔德在《福布斯》杂志上系统地叙述了梅特卡夫的关于网络代价指数增长的理念，即幻灯片里那条指数增长的曲线，并把它定名为“梅特卡夫定律”。其时美国互联网方才抽芽，种种网站都在快速增长，吉尔德的总结让“梅特卡夫定律”被科技界和互联网圈逐渐接管。不久之后，美国联邦通信委员会主席的里德·洪特（Reed E. Hundt）说：“摩尔定律和梅特卡夫定律”为我们提供了领略互联网的最佳角度” 。而之后马克·安德森创建了Netscape，宣布了网景欣赏器，用户数一路疾走，安德森在总结网景的飞速成长时，称“梅特卡夫定律是一盏明灯”。而之后跟着互联网在美国强势崛起，这个起初描写硬件网络代价的定律被外延到了整个互联网规模。无数网站的首创人将梅特卡夫定律写进了他们的贸易打算书，它在必然水平上成为无数互联网创业者和从业者的信念灯塔。
3COM公司曾用于销售推广的幻灯片（梅特卡夫展示原稿）
二、“梅特卡夫定律”的意义事实上，“梅特卡夫定律”在数学上是有意义的，一个N个节点的网络，它的总毗连数为N（N-1），当N足够大，它靠近于N²，假如把网络里的毗连数直接当作是网络的代价权衡指标，则“梅特卡夫定律”一个完全创立的等式。那么，在现实中是否是真的这样呢？2013年，梅特卡夫本人在《IEEE计较机》上颁发了一篇文章，用Facebook从10年的实际数据证明白本身的定律切合Facebook现实中的生长轨迹。有趣的是，同样在2013年，来自中国科学院的三位作者张兴洲、刘景洁、徐志伟也在著名的《计较机科学与技能》杂志上也颁发了一篇名为《Tencent and Facebook Data Validate Metcalfe’s Law》的论文。论文顶用腾讯和Facebook两个公司的数据验证了它们的月活数据和它们各自的估值（市值）是切合“梅特卡夫定律”的。（在“卫夕指北”公家号靠山回覆“腾讯”获取论文。）正是由于“梅特卡夫定律”的存在，让无数互联网人对局限和增长前仆后继，因为他们深刻地领略，局限能带来指数级的回报，这一回报凡是会超出正常的预期。事实上，梅特卡夫定律简直在表明无数互联网案例时都有着极强的说服力，举一个简朴的例子：为什么5G成为科技竞争博弈中要害中的要害？原因是其背后指数级的代价——第一代互联网接入的PC存量设备数约莫是10亿台，第二代移动互联网接入的智妙手机存量设备数约莫为30亿台，而5G成熟之后的IoT物联网时代，接入的数据守旧预计将到达500亿台，按照梅特卡夫定律由此发生的指数级代价是极其惊人的，某种意义上，这也是美国必然要封杀华为背后的重要逻辑。为什么滴滴、快的、Uber的打车战争会如此惨烈？为什么近些年风行行业老大归并行业老二？为什么自媒体的头部玩家会享受到这个行业最顶级的回报？为什么操纵系统市场凡是很能容下二个以上的玩家？.....这些问题都可以隐约在梅特卡夫定律中找到谜底。 三、“梅特卡夫定律”的争议尽量“梅特卡夫定律”对互联网的影响庞大，但业界依然对这个定理自己提出了差异的观点——2006年7月一位名为鲍勃·布里斯科的研究员就在《IEEE》上颁发了一篇立场光鲜的文章——《梅特卡夫定律是错误的》，他旌旗光鲜地指出梅特卡夫定律基础缺陷在于——对网络中的所有毗连都赋予了沟通的代价。“梅特卡夫定律”其实背后有两个埋没的假设——第一，网络的机制取决于网络之间相互毗连数的代价之和；第二，每一个毗连的代价是沟通的。布里斯科的这篇文章并没有质疑第一个假设，而是质疑了第二个假设，在他看来，网络中的毗连的代价并不是同等重要的，毗连也分强毗连和弱毗连，弱毗连的代价显然就没有强毗连那么大。甚至他还引用了作家梭罗《瓦尔登湖》里的一段话作为论据——“我们急于制作从缅因州到德克萨斯州的磁电报，可是缅因州和得克萨斯州之间和其他人口更多的州对比大概没有什么重要的交换。”没错，上述对梅特卡夫定律质疑从理论的角度是公道的，从现实中调查，我们也看到了和梅特卡夫定律相悖的现实，我随便举一个例子：一所精英大学原来一年招1000人，假如它扩充到2000人，它的代价和影响力会不会酿本钱来的4倍呢？或许率不会，这是很容易领略的，因为这个实际例子和梅特卡夫定律的抱负设定显然有不相符的处所——第一大学的代价和影响力并不直接有网络中的毗连数抉择。第二，多一倍的学生并不料味着他们会自动跟所有学生成立接洽。第三，扩招之后的学生质量或许率也会下降，因此毗连的代价自己也大概下降。很显然，梅特卡夫定律在详细的环境中并不能直接生搬套用，但我们又简直调查到了腾讯和Facebook的数据完美地证实了梅特卡夫定律。那么，应该如何领略这种悖论呢？在我看来，Facebook人数的增多，很显然毗连的质量是差异的，同时新插手的人也不行能和所有人成立毗连，但我们大概忽略了局限带来的其他外部效应——好比人数足够多之后的边际本钱低落，再好比人数足够多之后的数据积聚也会提高一个量级等。所以，“梅特卡夫定律”更多的是对一种现象的抽象，直接在任何互联网产物中生搬硬套都是教条的。正如经济学的基本成立在“理性人”这一假设之上，但实际中人却不老是理性的，事实上对付“理性人”假设的质疑降生了很多有代价的新经济理论。
四、另一个非线性增长的模子——齐普夫法例有趣的是，鲍勃·布里斯科在阐述“梅特卡夫定律”大概裂痕的同时，提出了一个新的描写网络代价和网络成员的法例——齐普夫法例。它以语言学家齐普夫定名，齐普夫在20世纪早期发明英文中词频的纪律——最常用的"The"占所有英文文本的7％，第二常用的单词"of"占比则3.5％，第三位的"and"占比为2.8％.......切合7%的1 倍、1 / 2倍、1 / 3倍……这一纪律。这一纪律用数学公式抽象为V=k*n log（n），既代价和数量呈对数干系。齐普夫法例是描写代价和数量更温和的模子，举个例子——如果一个网络10万人的时候代价100万，假如增加到20万人，按照梅特卡夫定律，它的代价增长到400万，但按照齐普夫法例的计较，它的代价则只增长到210万，留意，210万依然比200万这一线性增长的代价要更高。所以，尽量鲍勃·布里斯科指出了“梅特卡夫定律”大概存在的缺陷，但他却认可一个网络的代价和成员之间的干系并不是线性增长的，齐普夫法例也是一个非线性增长的模子。这两个模子都指向了一个原则——网络的毗连局限的晋升带来的回报是超预期的。那么现实世界中哪个模子是对呢？或者这个问题并没有谜底，但它们却从差异的层面给了我们领略这个真实世界的角度。这正是贸易世界有趣的处所，和严格的数学、物理学差异，贸易世界的纪律的合用受无数约束条件的节制，我们只能尽大概把握在大大都环境下都合用的纪律，必然要拿出一个反例去辩驳一条在大部门场景都普遍合用的贸易纪律其实没有意义。

所以，总结一下，梅特卡夫定律是对网络指数增长的普遍纪律的一种抽象，它汇报我们一个简朴的原理——局限的意义比你想象的越发的重要。作为互联网人，我们需要深刻领略梅特卡夫定律所代表的一种指数级增长逻辑，尽大概成立更多的毗连，从而在这个不确定的世界更好地保留。

——End——